A Generic Random Walk Metropolis-Hastings Algorithm

rwMHgen computes random draws of parameters using a normal proposal distribution. This function implements a generic form of RWMH

rwMHgen(start = NULL, posterior = NULL, ..., propob = NULL,
  const = NULL, seed = 1, vscale = 1.5, iter = 5000,
  burn = floor(0.1 * iter), report = NULL)

Arguments

start	starting values of parameters for the MH algorithm. It is automatically generated from the normal proposal distribution but the user can also specify.
posterior	the log posterior distribution function. Should take parameter input of the same length as start or propob$mode
...	additional arguments to the posterior function
propob	a list of mode and variance-covariance matrix of the normal proposal distribution. Write list as propob=list(mode=mode,var=variance-covariance)
const	a vector function of parameters showing non-negative inequality constraints to be satisfied.
seed	an integer as seed for reproducibility
vscale	a value multiplied by propob$var in order to adjust the proposal distribution. Else set to the character string "HS18" for the Herbst and Shorfheide (2018) scale updating for a 0.25 acceptance ratio. The default is 1.5 but the user can adjust it until a satisfactory acceptance rate is obtained.
iter	number of random draws desired (default: 5000)
burn	burn-in period for the MH algorithm (default: floor(0.1*iter))
report	a numeric frequency (i.e. after how many iterations to report progress) for reporting algorithm progress; default - NULL

Value

Matpram a matrix of parameter draws

postvals vector of posterior values corresponding to parameter draws Matpram

AcceptRatio the acceptance ratio

Examples

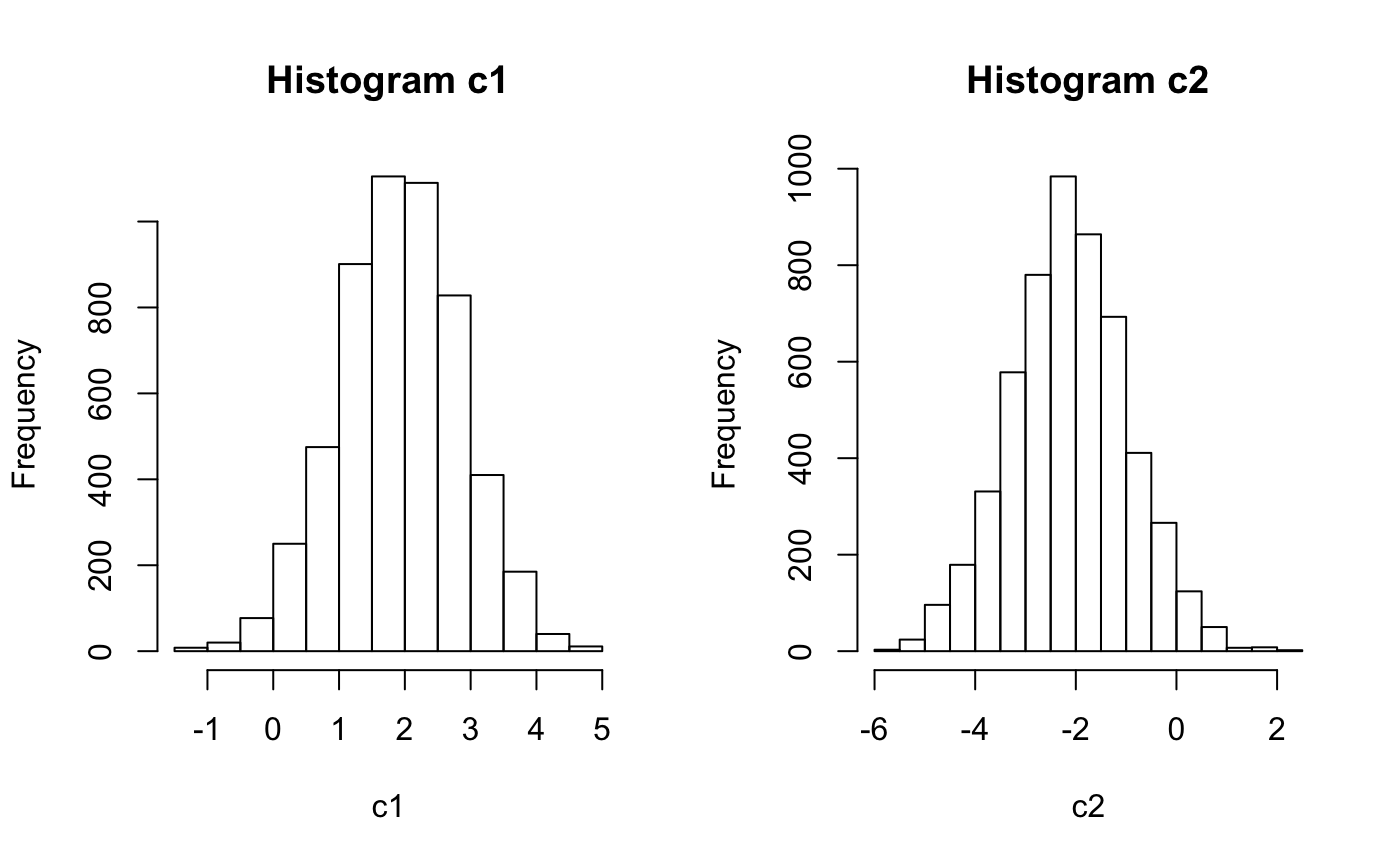
#a toy example for illustration
## f(c) = 1/(3.618*sqrt(pi))* exp(-0.6*(c[1]-2)^2-0.4*(c[2]+2)^2) 
# an improper posterior
logpost = function(c) -0.6*(c[1]-2)^2-0.4*(c[2]+2)^2 #log posterior distribution
optp<-optim(par=c(0,0),fn=logpost,control=list(fnscale=-1),hessian = TRUE)
# laplace approximation of the posterior
propob = list(mode=optp$par,var=-solve(optp$hessian)) #parameters of proposal distribution
eigen(propob$var)$values # var-cov of proposal distribution is positive definite
#> [1] 1.2500000 0.8333333
MHobj<- rwMHgen(posterior = logpost,propob = propob,vscale = "HS18",iter = 6000,report=1500)
#> 1500 iterations done. 4500 more to go. 
#> 3000 iterations done. 3000 more to go. 
#> 4500 iterations done. 1500 more to go. 
#> 6000 iterations done. 0 more to go. 
#> rwMHgen algorithm successful
# create an independent Metropolis-Hastings object
dim(MHobj$Matpram) # a 2 x 5000 matrix with columns corresponding to draws of c1 and c2
#> [1]    2 5400
par(mfrow=c(1,2))
hist(MHobj$Matpram[1,],20,main = "Histogram c1",xlab = "c1")
hist(MHobj$Matpram[2,],20,main = "Histogram c2",xlab = "c2"); par(mfrow=c(1,2))
MHobj$AcceptRatio # acceptance ratio
#> [1] 0.5488333